目录

P6.例5
P11.例4
p17.例14
p18.例17 没想到凑e的思路，以及简单的sinx~x没看出来
p19.例19 先推了一遍$\sqrt[n]{a}=e^0=1$,然后放在幂指函数分子里就看不出来它等于一了，还是要利用P18公式凑e,还利用了$\underset{x\to 0}{lim}\frac{a^x-1}{x}=lnx$这个等价无穷小，题目中化成$\underset{x\to \mathrm{\infty }}{lim}\frac{\sqrt[n]{a}-1}{\frac{1}{n}}=lnx$,没看出来$\sqrt[n]{a}=a^{\frac{1}{n}}$
p22.例24 凑成了等价无穷小相加的形式，但是对相加的代换不熟悉，认为不能代换，于是思路卡住
p23.例25 没有凑等价无穷小的思路，使用洛必达算到倒数第二步的时候，不敢直接把常数项算出来（奇奇怪怪）
p24.例27，首先要把多项式里能直接算出极限的算出来，再看另外一部分，不知道a=1是哪来的，凑个$e^{\frac{1}{x}}-1$
p25.例28思路混乱，没有利用到极限存在，分子为0，分母也为0,取特殊值瞎猫碰到死耗子对了
p25.例29 x<0 答案提的是-x,我提的是x,原因因为要变号，可以用t=-x代换，或者这么想，把根号里变成两部分，对其中一部分开算数平方，那个值肯定是正的，由于x<0,所以$\sqrt{x^2}=(-x)$
p26.例30，计算时分母的分数直接拿出去了，没取倒数，导致计算错误，stupid error
$\sqrt{x^2}=(-x)$
p26.例31,拿到题目就开始洛，然后洛了一次后感觉更复杂了不想求导了，原因在于$(1-x^2）$和tan...没有拆开得到完全平方和sin cos，从而得到非零因子，把非零因子提前计算出来简化运算
p27.例32,由于对$ln(x+\sqrt{1+x^2})\mathrm{的}\mathrm{导}\mathrm{数}$不熟悉，求导后推得乱七八糟，放弃了，对于这种常见结论不熟悉导致的，如果记住了就没有这么多事，不记住的话要拆分后递归计算，不然全混在一起会导致式子特别复杂，缺乏计算的欲望，利用编程里递归的思想，可以把分子分母而治之再带入
p27.例33发散思维洛了一次，看到以前记的只能洛到一阶导，去用导数的定义写了f''(0)相关的式子，然后离答案就差一步，比较洛一次的原式子与f''(0)的式子发现他们俩只是差一个系数的关系，差点做出来了...还有一种思路是看到f(0)和f'(0)和f''(0),马上想到泰勒公式的定义，用它们把f(x)构造出来
p.28.例34 用泰勒做的，公式先是展开cosx的时候多了一项$x^3$的，自己发现了，然后依然计算出一个错的值，因为抄展开后的式子把加号写减号了，差一点对，目前战绩八连败了哈哈哈，看第二种洛必达的方法，洛了一次后想凑x-sinx和$e^x-1$,思路跟答案一样，但是发现凑不出来，打算洛第二次感觉太复杂，看答案思路没问题，是求导cosx时漏了个负号，于是再计算，又出符号问题，凑+x-x变成了+x+x，可以算九连败了，匹配机制该发力了
p31.例38 只记得这种题目有个通用的结论但不记得怎么推导，看答案后整理思路：找到里面的最大项，利用小于一分数的无穷次方等于零把其他项消掉，如果要使用夹逼定理，右边取n个最大项，左边取一个最大项而不是n个最小项，这样放缩的原理是除了最大项其它的项都能被消掉
p32.例41,最后总结的时候多了一个x<0的情况，题目中明确说了x>0
p32.例42 没有证明极限存在就直接求极限，然后$\frac{1}{2}$后的括号抄丢了导致极限求错,为什么要证明极限存在，因为等式两边同时取极限的前提是等式两边的极限存在，如果这题10分，求极限只能占两分，使用单调有界数列必有极限，先使用$a^2+b^2\ge 2ab$这个基本不等式得到$x_n$，然后再使用$x_n$的值带入，使用两式想比或相减得到数列单调性，反例1,0,1,0,1,0...这个数列两边取极限可以求得极限值，但实际这个数列无极限
p35.例48 错题索引#p35.例48
p36.例1 把$cos\sqrt{x}\mathrm{当}\mathrm{成}\mathrm{了}co{s}^{\frac{1}{2}}x$从而导致计算错误
p36.例2 在进行洛必达时，求导中$e^{2ax}$漏掉了a这个系数变成了$e^{2ax}\times 2$,导致错误
p37.例3 使用画图法做对了 其中三次方程的解法有点不好想到三次方程
p37.例4 找间断点的时候不知道怎么想的取了让ln为0 |x|=1 而不是|x| = 0,x->1的间断点算对了，另一个因为x->-1在连续段算出来一个可去间断点，实际要算x->0点的两段极限，瞎猫碰死耗子把答案选对了
p39.例7 找间断点的时候取大分母等于0，然后抄错条件（e的指数的分子上的x抄成了0）导致没有第一个间断点，第二个间断点$\frac{1}{-\mathrm{\infty }}$被我直接当成$-\mathrm{\infty }$了，大错特错
p40.例8 在x->0这个间断点的时候 $sin(\frac{1}{x})\to sin\mathrm{\infty }$,不是趋于零，误使用等价无穷小变成$\frac{1}{x}$了，实际是有界乘以无穷小等于无穷小
[[#p41.例9]]p41.例9 对这种类型的函数不熟悉，实际上是类比$\underset{n\to \mathrm{\infty }}{lim}{x}_n$的极限对f(x)的表达式求出来，然后再根据函数图像看间断点
p41.例10 证明题 没有思路 看了答案整理了一下思路，首先求出f($ϵ$)的表达式，然后在闭区间内根据f($ϵ$)表达式的结构，把区间内最大值最小值表示成对应的形式比大小，然后得到这个表达式在最大值最小值之间，然后根据高数#闭区间上连续函数的性质介值定理，得到f($ϵ$)必定存在

p32.例1 求一点的左导数没问题，求右导数时f(1)把1代入了$x^2$的表达式，属于书上写的经典错误,定义左右导数写的是$\underset{\mathrm{\Delta }x\to 0^{+}}{lim}\frac{f(x_0+\mathrm{\Delta }x)-f(x_0))}{\mathrm{\Delta }x}\mathrm{而}\mathrm{不}\mathrm{是}\underset{\mathrm{\Delta }x\to 0^{+}}{lim}\frac{f(x_0+\mathrm{\Delta }x)-f(x_0^{+}))}{\mathrm{\Delta }x}$,取得是那一点在定义上的函数值而不是在那一点的左右极限值，本题还可以通过非右连续性证明在这一点不可导
p46.例5 没有利用到可导一定连续求出f(0) 对于高阶无穷小理解出错 把1/x当成无穷小（0）了
p48.例7 对$si{n}^2\frac{1}{x}$求导出错，原因在于这是一个三层复合，我把第二层的$cos(\frac{1}{x})$写丢了
p46.例9 负的括号展开的时候里面的+号没变号 又是一个little error (出现频率太多了)
p50.例11 对二阶导的计算公式记忆错误，少求了一阶导对于t的导数
p51.例12 题目求微分，求完导数忘了乘以dx
p51. 例13 取ln后对ln的基本运算法则不熟悉 没有把ln(ab/cd)拆成lna+lnb-lnc-lnd,所以硬求得出来一个复杂的式子，不知道对不对
p52. 例15 使用莱布尼茨公式求出来一个式子，也知道$x^2$求二阶导后就变为零，对二项式定理不熟悉，没有把它展开，对排列组合数不熟悉，刚好抖音博主讲故事的藜菽微积分第12集讲了这个，晚上看
p55.例23 错误原因：算到最后一步把分母的$(2e^t+1{)}^2\mathrm{写}\mathrm{成}\mathrm{了}2e^t$然后导致最终答案算错
p56.例24 错误原因：把$(-1{)}^n\mathrm{与}{2}^n$相城，误得到了$2^{-n}$,没有想到把前面一串化成阶乘的形式
p58.例28 错误原因 分子分母都有$e^{\theta }$次方应该约掉，我给提出来了，然后乘法求导我给写成减号了，导致斜率全错
p58.例29 对变化率的理解不够 把它当成了比值然后化成了极坐标求解 然后答案理所当然错了，变化率应该是导数
p54.例19D选项没继续算，实际上是得到一个带|x|的极限式子，左右极限不相等
p55.例20 B.C选项的疑惑 不行是因为分子上两个都是动点，不满足导数定义的一定一动 可以拿y=|x|当做C选项的反例，如果凑加减项

P67.例6 把1-cosx等价为-1/2x^2了...,导致导数正负判断相反。。。没有想到保号性判断极值
P.67.例7 思路对的，最后计算出错 分母27*3算成了71 填空题啊啊啊 一分没有

题目

p35.例48

错误思路
$\begin{array}{c}\underset{x\to 0}{lim}\frac{ax+b{x}^2+\ln (1+x)}{e^{x^2}-\cos x}=1\\ =\frac{ax+b{x}^2+x}{e^{x^2}-1+1-\cos x}\\ =\frac{(a+1)x+b{x}^2}{x^2+\frac{x^2}{2}}\\ =\frac{(a+1)x+b{x}^2}{\frac{3x^2}{2}}\\ a+1=0\\ b=\frac{3}{2}\\ a=-1\end{array}$

• 分子展开不足：仅展开 ln(1+x) 到一阶（x），忽略二次项（−2x2​），导致分子二次项系数计算错误。
• ​系数匹配错误：未正确匹配分子分母的同次幂项，导致 b 的解答错误。

p37.例3

三次方程解法
$\begin{array}{rl}& c^3+c=2\\ & c^3-1^3+c-1=2\\ & \because a^3-b^3=(a^2+ab+b^2)\\ & \therefore (c-1)(c^2+c+1)+(c-1)=0\\ & (c-1)(c^2+c+2)=0\\ & a^3-b^3=(a^2+ab+b^2)\end{array}$

p41.例9

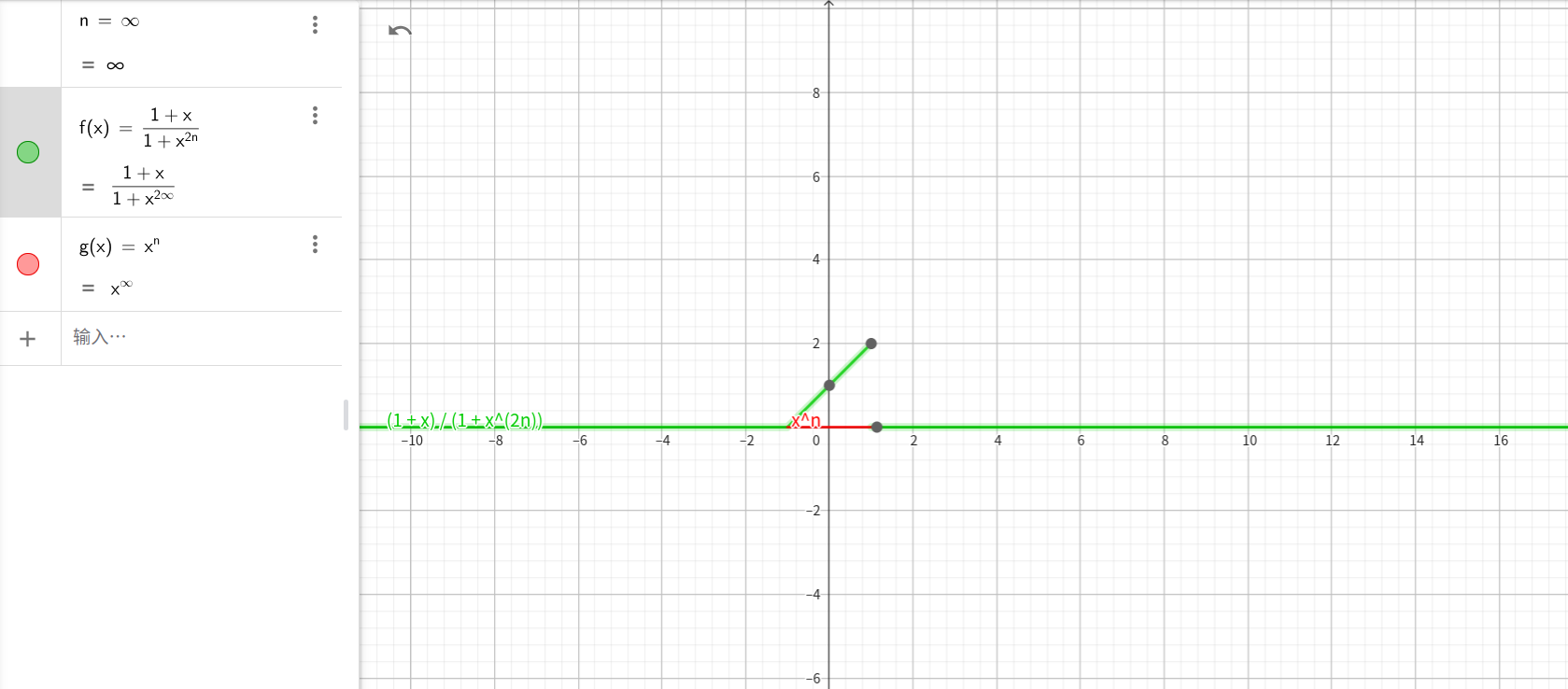
看到求带$x^n$的极限的时候要想到这个公式