第一章 函数 极限 连续
复合函数
条件:外函数定义域与内函数值域交集不为空
反函数
存在反函数条件:对于一个函数,一个y只能有一个唯一对应的x
单调函数一定有反函数 反之不然
arccosx取得是 cosx 定义域
奇偶性
求奇偶性 可以用f(-x)+f(x)=0的变形
奇函数 0点处若有定义则f(0)=0
周期性
有界性
无界函数的定义:
p6.例5 利用三角函数周期性消除有界变量的影响
数列极限
- 如果对于任意的
,总存在正整数N,当n>N时,恒有 成立,则称常数a为数列{ }当n趋于正无穷时的极限,记为 -
-> 绝对值不等式
函数极限
- 自变量趋于无穷大
对于任意给定的,总存在X>0,当|x|>X,时恒有|f(x) - A|< ,则称常数A为f(x)当x-> 时的极限,记为 的极限,记为
做题时分解为 和 - 自变量趋于有限值
对于任意给定的,总存在 ,当 ,恒有|f(x) - A|< ,则称常数A为f(x)当x-> 时的极限,记为 的极限,记为
做题时分解为 和 - 需要考虑分段的函数
- 分段函数的分段点(包括带绝对值的函数)
型 型、
p.11例4思路错误,首先把arctan的极限当成了+_1,其次把 的值当成1,错误原因在于 是个 型极限,要使用 计算,或参考p18方法1 2.的结论
极限的性质
与极限相关有界性:
高数#有界性
- 数列:
如果数列{}收敛(有极限),那么数列{ }一定有界
反之不成立,如 - 函数:
若存在,则f(x)在 某去心邻域有界(局部有界)
反之不存在,如:
与极限相关保号性:
应用:根据保号性求极值
极限值与无穷小之间关系:
极限的存在准则
夹逼
取整函数基本不等式
单调有界数列必有极限
无穷小量
比较无穷小的时候就要用等价无穷小代换
无穷小性质
有限个无穷小的和(积)仍为无穷小
无穷小量与有界量的积仍为无穷小
无穷大量
定义:
常用比较
- 函数
- 数列
性质:
- 有限个个无穷大量的积仍为无穷大量
- 无穷大量与有界变量之和仍为无穷大量,不要误以为无穷大与有界之积为无穷大
与无界变量关系:
与无穷小量关系:互为倒数,但f(x)(分母)不能为0
例14
求极限
- 利用基本极限求极限
- 利用等价无穷小代换求极限
原则:乘除关系可以换,加减关系在一定条件下可以换
相减时,被替换的被减数和减数不能是同阶无穷小,且比值不能等于1
相加时,被替换的被减数和减数不能是同阶无穷小,且比值不能等于-1 - 利用有理运算法则求极限
- 利用洛必达法则求极限
洛必达法则:
若
则 - 使用夹逼准则求极限
- 利用单调有界准则求极限
- 利用定积分定义求极限
无穷小量阶的比较
函数的连续性
定义理解:函数在一点处的极限值等于函数值,则称函数在这一点连续,区间上每个点都连续称函数在这个区间内连续
间断点及其分类跳跃间断点
定义理解:在一点左右(去心邻域)有定义,在这个点不连续
第一类间断点
左右极限都存在的间断点
- 可去间断点 左右极限相等
- 跳跃间断点 左右极限不等
第二类间断点
左右极限至少有一个不存在 - 无穷间断点 左极限或右极限为无穷
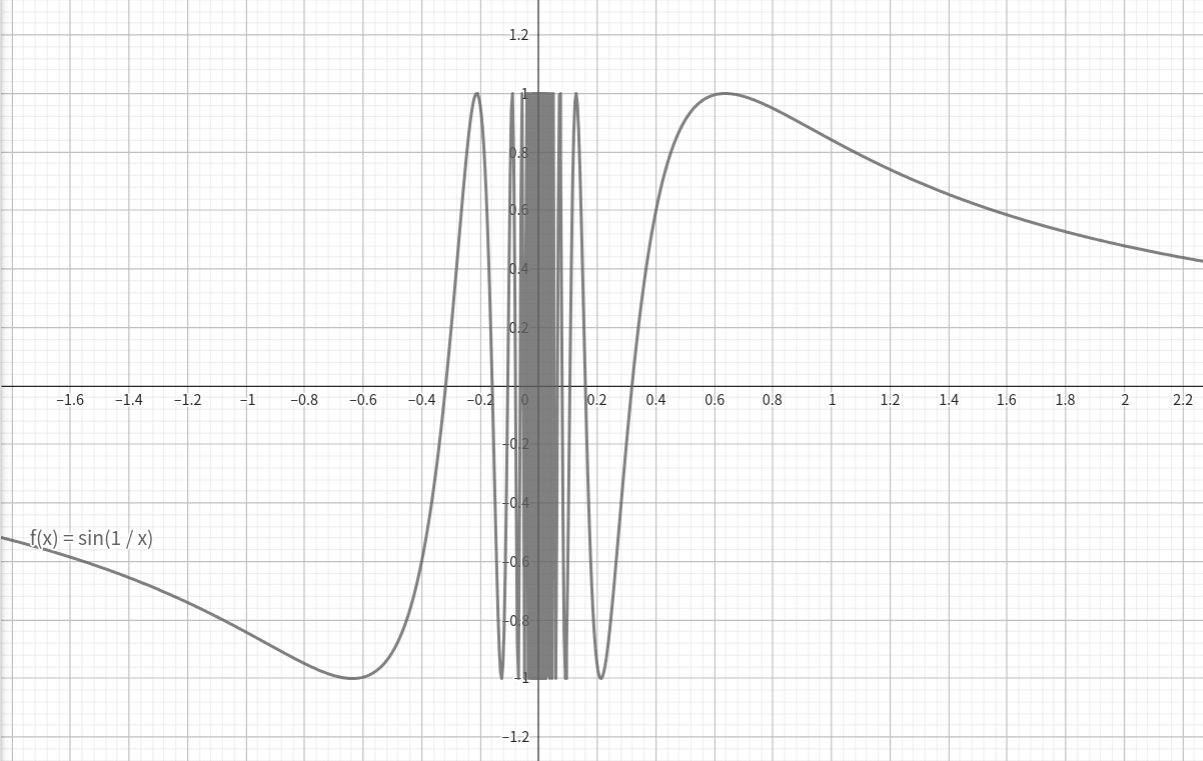
- 振荡间断点
连续性的运算与性质
闭区间上连续函数的性质
最值定理:
有界性定理:
介值定理:
推论:
零点定理:
重要应用:证明方程根的存在性?
第二章 导数与微分
导数与微分的概念
导数 定义:设函数f(x)在
微分 定义:设函数f(x)在点
导数与微分的几何意义
法线与切线成90度夹角
微分的几何意义:
微分dy在几何上表示函数切线上的增量
graph TD
%% 定义节点
A[连续] -.不一定.-> B[可导]
B -->A
B -.一元函数.-> C[可微]
C --> B
A -.不一定.-> C
C --> A
%% 调整布局方向为左右循环,形成三角关系
classDef default fill:#f9f,stroke:#333;
classDef cond fill:#ccf,stroke:#333;
classDef smooth fill:#9f9,stroke:#333;
class A,B,C default
linkStyle 0 stroke:#333,stroke-width:2px
linkStyle 1 stroke:#333,stroke-width:2px
linkStyle 2 stroke:#f00,stroke-width:2px,stroke-dasharray:5,5
如
导数公式及求导公式:
基本初等函数求导公式
3.利用
(13) 14. 15. 16.使用反函数求导的公式
求导法则
- 有理运算法则
- 复合函数求导
- 隐函数求导法
- 反函数的导数
- 参数方程求导法 (利用反函数的导数结论推导)
- 对数求导法
高阶导数
常用公式
充分必要
微分中值定理
费马引理
极值点处可导且导数值为0,反例f(x)=|x|
罗尔定理
闭区间连续 开区间可导 区间端点处函数值相等
-> 开区间内必有一点导数值为0
拉格朗日中值定理
闭区间连续 开区间可导
-> 开区间内必有一点的切线与两端点的连线平行
柯西中值定理
f(X) F(X) 闭区间连续 开区间可导
F‘(x)在开区间内处处不为0 (保证分母不为零)
对参数方程g(x) y=f(t) x=F(t)
参数方程在开区间内必有一点的切线与两端点的连续平行
泰勒公式
【【官方双语】微积分的本质 - 10 - 泰勒级数-哔哩哔哩】 https://b23.tv/Ln1UwWU
导数应用
单调性
极值
求极值:找驻点和导数不存在的点
两个充分一个必要条件:?
导数为0的点称为函数的驻点
最值
求闭区间内最值:找极值,找端点值,比较大小
若有唯一极值点,就是最值点,不用与端点值比较
凹凸性
函数在区间上连续,区间内任意两点的连线的中点,大于在这个两点横坐标中点的函数值,则称图形在区间内是凹的,反之是凸的
凹与凸的分界点称为拐点。它是点的坐标(
拐点
拐点的两个充分一个必要条件就是把极值的向上升一阶
?
渐近线
- 水平渐近线
- 垂直渐近线
- 斜渐近线
水平渐近线和斜渐近线在一侧或 一侧不可能同时存在
曲线的弧微分与曲率
弧微分
曲率
曲率半径